Updated the paper (CLion plsfix the math markdown)

README.md

@@ -42,7 +42,7 @@ The Product Key itself (not to confuse with the RPK) is of form `FFFFF-GGGGG-HHH
 the alphabet `BCDFGHJKMPQRTVWXY2346789` to exclude any characters that can be easily confused, like `I` and `1` or `O` and `0`.
 
 As per the alphabet capacity formula, the key can at most contain 114 bits of information.
-$$N = log2(24^25) ~ 114$$
+$$N = \log_2(24^{25}) \approx 114$$
 
 Based on that calculation, we unpack the 114-bit Product Key into 4 ordered segments:
 
@@ -71,11 +71,13 @@ They differ only slightly. Both curves are defined over the finite field, F<sub>
 F<sub>2m</sub> assumes $p = 2m$. Microsoft used the latter in their algorithm.
 
 An elliptic curve over the finite field F<sub>p</sub> consists of:
-* a set of integer coordinates ${x, y}$, such that $0 <= x, y < p$;
+* a set of integer coordinates ${x, y}$, such that $0 \le x, y < p$;
 * a set of points $y^2 = x^3 + ax + b \mod p$.
 
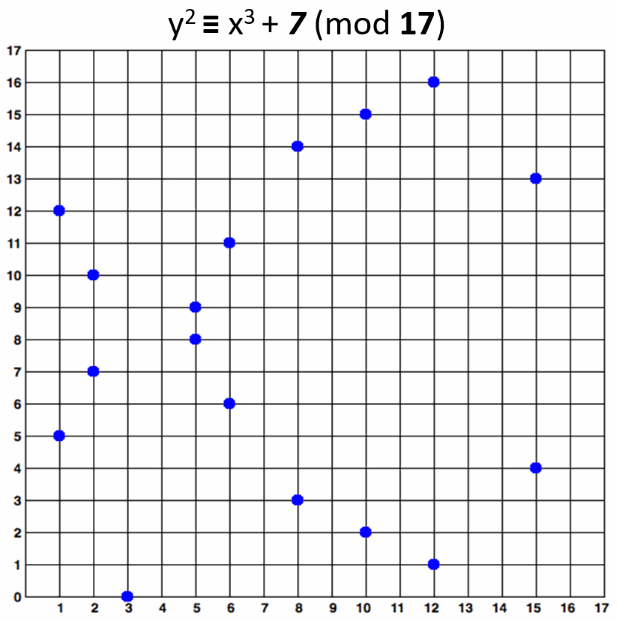
 **An elliptic curve over F<sub>17</sub> would look like this:**
 
+![F17 Elliptic Curve](https://user-images.githubusercontent.com/44542704/230788993-d340f63c-7201-4307-a52c-9bf159b99d02.png)
+
 The curve consists of the blue points in above image. In practice the "elliptic curves"
 used in cryptography are "sets of points in square matrix".
 
@@ -95,9 +97,9 @@ To create the CD-key generation algorithm we must compute the corresponding priv
 which means we have to reverse-solve the one-way ECC task. 
 
 Judging by the key exposed in BINK, p is a prime number with a length of **384 bits**.
-The computation difficulty using the most efficient Pollard's Rho algorithm ($O(\sqrtn)$) would be at least $O(2^168)$, but lucky for us,
+The computation difficulty using the most efficient Pollard's Rho algorithm ($O(\sqrt{n})$) would be at least $O(2^{168})$, but lucky for us,
 Microsoft limited the value of the signature to 55 bits in order to reduce the amount of matching product keys, reducing the difficulty
-to a far more manageable $O(2^28)$.
+to a far more manageable $O(2^{28})$.
 
 The private key was, of course, conveniently computed before us in just 6 hours on a Celeron 800 machine.