endermanch
/
XPKeygen
1
0
Fork 0
Code Issues 11 Pull Requests 1 Packages Projects Releases 8 Wiki Activity

Updated the paper (CLion plsfix the math markdown)

This commit is contained in:
Andrew 2023-04-09 21:04:00 +03:00 committed by GitHub
parent 8459d61f47
commit 23ce5f10ef
No known key found for this signature in database
GPG Key ID: 4AEE18F83AFDEB23
1 changed files with 6 additions and 4 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

10
README.md
View File

@ -42,7 +42,7 @@ The Product Key itself (not to confuse with the RPK) is of form `FFFFF-GGGGG-HHH
the alphabet `BCDFGHJKMPQRTVWXY2346789` to exclude any characters that can be easily confused, like `I` and `1` or `O` and `0`. the alphabet `BCDFGHJKMPQRTVWXY2346789` to exclude any characters that can be easily confused, like `I` and `1` or `O` and `0`.
As per the alphabet capacity formula, the key can at most contain 114 bits of information. As per the alphabet capacity formula, the key can at most contain 114 bits of information.
$$N = log2(24^25) ~ 114$$ $$N = \log_2(24^{25}) \approx 114$$
Based on that calculation, we unpack the 114-bit Product Key into 4 ordered segments: Based on that calculation, we unpack the 114-bit Product Key into 4 ordered segments:
@ -71,11 +71,13 @@ They differ only slightly. Both curves are defined over the finite field, F<sub>
F<sub>2m</sub> assumes $p = 2m$. Microsoft used the latter in their algorithm. F<sub>2m</sub> assumes $p = 2m$. Microsoft used the latter in their algorithm.
An elliptic curve over the finite field F<sub>p</sub> consists of: An elliptic curve over the finite field F<sub>p</sub> consists of:
* a set of integer coordinates ${x, y}$, such that $0 <= x, y < p$; * a set of integer coordinates ${x, y}$, such that $0 \le x, y < p$;
* a set of points $y^2 = x^3 + ax + b \mod p$. * a set of points $y^2 = x^3 + ax + b \mod p$.
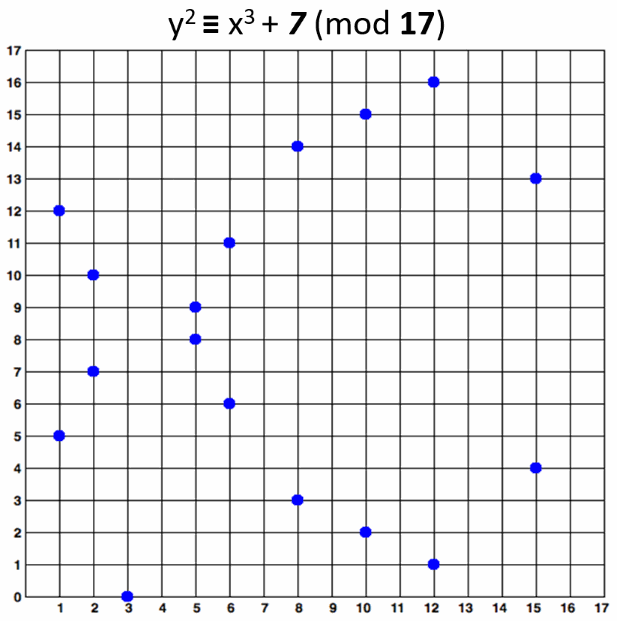
**An elliptic curve over F<sub>17</sub> would look like this:** **An elliptic curve over F<sub>17</sub> would look like this:**
![F17 Elliptic Curve](https://user-images.githubusercontent.com/44542704/230788993-d340f63c-7201-4307-a52c-9bf159b99d02.png)
The curve consists of the blue points in above image. In practice the "elliptic curves" The curve consists of the blue points in above image. In practice the "elliptic curves"
used in cryptography are "sets of points in square matrix". used in cryptography are "sets of points in square matrix".
@ -95,9 +97,9 @@ To create the CD-key generation algorithm we must compute the corresponding priv
which means we have to reverse-solve the one-way ECC task. which means we have to reverse-solve the one-way ECC task.
Judging by the key exposed in BINK, p is a prime number with a length of **384 bits**. Judging by the key exposed in BINK, p is a prime number with a length of **384 bits**.
The computation difficulty using the most efficient Pollard's Rho algorithm ($O(\sqrtn)$) would be at least $O(2^168)$, but lucky for us, The computation difficulty using the most efficient Pollard's Rho algorithm ($O(\sqrt{n})$) would be at least $O(2^{168})$, but lucky for us,
Microsoft limited the value of the signature to 55 bits in order to reduce the amount of matching product keys, reducing the difficulty Microsoft limited the value of the signature to 55 bits in order to reduce the amount of matching product keys, reducing the difficulty
to a far more manageable $O(2^28)$. to a far more manageable $O(2^{28})$.
The private key was, of course, conveniently computed before us in just 6 hours on a Celeron 800 machine. The private key was, of course, conveniently computed before us in just 6 hours on a Celeron 800 machine.