From 5a3105ecbd31ffe0474e5e7276dc685af25d0187 Mon Sep 17 00:00:00 2001 From: Andrew <44542704+Endermanch@users.noreply.github.com> Date: Sun, 28 May 2023 14:22:39 +0300 Subject: [PATCH 01/11] Update README.md --- README.md | 8 +++----- 1 file changed, 3 insertions(+), 5 deletions(-) diff --git a/README.md b/README.md index 450c578..569c995 100644 --- a/README.md +++ b/README.md @@ -68,15 +68,13 @@ Based on that calculation, we unpack the 114-bit Product Key into 4 ordered segm | Segment | Capacity | Data | |-----------|----------|-------------------------------------------| -| Flag | 1 bit | Reserved, always set to `0x01`* | +| Upgrade | 1 bit | Upgrade version flag | | Serial | 30 bits | Raw Product Key (RPK) | | Hash | 28 bits | RPK hash | | Signature | 55 bits | Elliptic Curve signature for the RPK hash | -For simplicity' sake, we'll combine `Flag` and `Serial` segments into a single segment called `Data`. By that logic we'll be able to extract the RPK by -shifting `Data` right and pack it back by shifting bits left. - -*It's not fully known what that bit does, but all a priori valid product keys I've checked had it set to 1. +For simplicity' sake, we'll combine `Upgrade` and `Serial` segments into a single segment called `Data`. By that logic we'll be able to extract the RPK by +shifting `Data` right and pack it back by shifting bits left, because most a priori valid product keys I've checked had the Upgrade bit set to 1. ### Elliptic Curves From fd0f9669b49aecb1cca6360e57a907ef059dfe88 Mon Sep 17 00:00:00 2001 From: Andrew <44542704+Endermanch@users.noreply.github.com> Date: Sun, 28 May 2023 14:37:14 +0300 Subject: [PATCH 02/11] Update README.md --- README.md | 28 +++++++++++++--------------- 1 file changed, 13 insertions(+), 15 deletions(-) diff --git a/README.md b/README.md index 569c995..7b8d532 100644 --- a/README.md +++ b/README.md @@ -1,6 +1,6 @@ # XPKeygen -A Windows XP / Windows Server 2003 VLK key generator. This tool allows you to generate _valid Windows XP keys_ based on the _raw product key_, which can be random. -The **Raw Product Key (RPK)** is supplied in a form of 9 digits `XXX-YYYYYY` and is only necessary to generate a Windows XP Key. +A Windows XP / Windows Server 2003 VLK key generator. This tool allows you to generate _valid Windows XP keys_ based on the _Raw Product Key_, which can be random. +The **Raw Product Key (RPK)** is supplied in form of 9 digits `XXX-YYYYYY` and is only necessary to generate a Windows XP Key. ![image](https://user-images.githubusercontent.com/44542704/231724854-4517f3a1-2330-4e70-83ae-6c52fa1b4745.png) @@ -35,24 +35,22 @@ We need to use a random Raw Product Key as a base to generate a Product ID in a ### Product ID -| Digits | Meaning | -|-------:|:-------------------------------------------------------| -| AAAAA | OS Family constant | -| BBB | Most significant 3 digits of the RPK | -| CCCCCC | Least significant 6 digits of the RPK | -| S | Check digit | -| DD | Index of the public key used to verify the Product Key | -| EEE | Random 3-digit number | +| Digits | Meaning | +|-------:|:----------------------| +| AAAAA | OS Family constant | +| BBB | Channel ID | +| CCCCCC | Sequence Number | +| S | Check digit | +| DD | Public key index | +| EEE | Random 3-digit number | + The OS Family constant `AAAAA` is different for each series of Windows XP. For example, it is 76487 for SP3. - -The `BBB` and `CCCCCC` sections essentially directly correspond to the Raw Product Key. If the RPK is `XXXYYYYYY`, these two sections -will transform to `XXX` and `YYYYYY` respectively. - +The `BBB` and `CCCCCC` sections essentially encode the Raw Product Key. For example, if the first section is equal to `XXX` and the second section is equal to `YYYYYY`, the Raw Product Key will be encoded as `XXX-YYYYYY`. The check digit `S` is picked so that the sum of all `C` digits with it added makes a number divisible by 7. The public key index `DD` lets us know which public key was used to successfully verify the authenticity of our Product Key. -For example, it's 22 for Professional keys and 23 for VLK keys. +For example, it's `22` for Professional keys and `23` for VLK keys. A random number `EEE` is used to generate a different Installation ID each time. From 6e973f5c549f5e9e3829d2e4fdd43c5f96551026 Mon Sep 17 00:00:00 2001 From: Andrew <44542704+Endermanch@users.noreply.github.com> Date: Sun, 28 May 2023 14:37:59 +0300 Subject: [PATCH 03/11] Update README.md --- README.md | 2 ++ 1 file changed, 2 insertions(+) diff --git a/README.md b/README.md index 7b8d532..5519f0b 100644 --- a/README.md +++ b/README.md @@ -46,7 +46,9 @@ We need to use a random Raw Product Key as a base to generate a Product ID in a The OS Family constant `AAAAA` is different for each series of Windows XP. For example, it is 76487 for SP3. + The `BBB` and `CCCCCC` sections essentially encode the Raw Product Key. For example, if the first section is equal to `XXX` and the second section is equal to `YYYYYY`, the Raw Product Key will be encoded as `XXX-YYYYYY`. + The check digit `S` is picked so that the sum of all `C` digits with it added makes a number divisible by 7. The public key index `DD` lets us know which public key was used to successfully verify the authenticity of our Product Key. From fa6d8177bfbec54d5b19e0e1e4472122a01858b0 Mon Sep 17 00:00:00 2001 From: Andrew <44542704+Endermanch@users.noreply.github.com> Date: Sun, 28 May 2023 15:17:56 +0300 Subject: [PATCH 04/11] Update README.md --- README.md | 66 ++++++++++++++++++++++++++++++++++++++++++++++++++++++- 1 file changed, 65 insertions(+), 1 deletion(-) diff --git a/README.md b/README.md index 5519f0b..c61e834 100644 --- a/README.md +++ b/README.md @@ -58,7 +58,7 @@ A random number `EEE` is used to generate a different Installation ID each time. ### Product Key -The Product Key itself (not to confuse with the RPK) is of form `FFFFF-GGGGG-HHHHH-JJJJJ-KKKKK`, encoded in Base-24 with +The Product Key itself (not to confuse with the RPK) is in form `FFFFF-GGGGG-HHHHH-JJJJJ-KKKKK`, encoded in Base-24 with the alphabet `BCDFGHJKMPQRTVWXY2346789` to exclude any characters that can be easily confused, like `I` and `1` or `O` and `0`. As per the alphabet capacity formula, the key can at most contain 114 bits of information. @@ -103,11 +103,75 @@ used in cryptography are "sets of points in square matrix". The above curve is "educational". It provides very small key length (4-5 bits). In real world situations developers typically use curves of 256-bits or more. +### BINK resource Since it is a public-key cryptographic system, Microsoft had to share the public key with their Windows XP release to check entered product keys against. It is stored within `pidgen.dll` in a form of a BINK resource. The first set of BINK data is there to validate retail keys, the second is for the OEM keys respectively. +The structure of the BINK resource for Windows 98 and Windows XP is as follows: + +| Offset | Value | +|-------:|--------------------------------------------------| +| `0x0000` | BINK ID | +| `0x0004` | Size of BINKEY structure in bytes | +| `0x0008` | Header length | +| `0x000C` | Checksum | +| `0x0010` | Number-encoded date (BINKEY version) | +| `0x0014` | ECC curve order size (always `12` in practice) | +| `0x0018` | Hash length (always `28` in practice) | +| `0x001C` | Signature length (always `55` in practice) | +| `0x0020` | Finite Field Order `p` | +| `0x005C` | Curve Parameter `a` | +| `0x0098` | Curve Parameter `b` | +| `0x00D4` | Base Point x-coordinate `Gx` | +| `0x0110` | Base Point y-coordinate `Gy` | +| `0x014C` | Public Key x-coordinate `Kx` | +| `0x0188` | Public Key y-coordinate `Ky` | + +![BINK](https://github.com/Endermanch/XPKeygen/assets/44542704/497ad018-884f-41af-ba89-633202d30328) + +And here's my implementation for the BINK Reader in C: +```c +typedef struct _EC_BYTE_POINT { + CHAR x[256]; // x-coordinate of the point on the elliptic curve. + CHAR y[256]; // y-coordinate of the point on the elliptic curve. +} EC_BYTE_POINT; + +typedef struct _BINKHDR { + // BINK version - not stored in the resource. + ULONG32 dwVersion; + + // Original BINK header. + ULONG32 dwID; + ULONG32 dwSize; + ULONG32 dwHeaderLength; + ULONG32 dwChecksum; + ULONG32 dwDate; + ULONG32 dwKeySizeInDWORDs; + ULONG32 dwHashLength; + ULONG32 dwSignatureLength; + + // Extended BINK header. (Windows Server 2003+) + ULONG32 dwAuthCodeLength; + ULONG32 dwProductIDLength; +} BINKHDR; + +typedef struct _BINKDATA { + CHAR p[256]; // Finite Field order p. + CHAR a[256]; // Elliptic Curve parameter a. + CHAR b[256]; // Elliptic Curve parameter b. + + EC_BYTE_POINT G; // Base point (Generator) G. + EC_BYTE_POINT K; // Public key K. +} BINKDATA; + +typedef struct _BINKEY { + BINKHDR header; + BINKDATA data; +} BINKEY; +``` + In case you want to explore further, the source code of `pidgen.dll` and all its functions is available within this repository, in the "pidgen" folder. ### Generating valid keys From 840d951de81e7167ac0023400a923058562ae90e Mon Sep 17 00:00:00 2001 From: Andrew <44542704+Endermanch@users.noreply.github.com> Date: Sun, 28 May 2023 15:36:34 +0300 Subject: [PATCH 05/11] Update README.md --- README.md | 40 ++++++++++++++++++++++++++++++++++++++-- 1 file changed, 38 insertions(+), 2 deletions(-) diff --git a/README.md b/README.md index c61e834..48a7dda 100644 --- a/README.md +++ b/README.md @@ -76,6 +76,22 @@ Based on that calculation, we unpack the 114-bit Product Key into 4 ordered segm For simplicity' sake, we'll combine `Upgrade` and `Serial` segments into a single segment called `Data`. By that logic we'll be able to extract the RPK by shifting `Data` right and pack it back by shifting bits left, because most a priori valid product keys I've checked had the Upgrade bit set to 1. +Microsoft redid their Product Key format with Windows Server 2003 to include a backend server authentication key, which was an actually secure approach to +license validation, as no one could ever make a guess on which validation algorithm they had employed on their private server. Besides adding the online +validation mechanism, they also cranked up the overall arithmetic from 384 to 512 bits, and the signature scalar to 62 bits of information. + +| Segment | Capacity | Data | +|------------|----------|-------------------------------------------| +| Upgrade | 1 bit | Upgrade version flag | +| Channel ID | 10 bits | The `BBB` part of the RPK | +| Hash | 31 bits | RPK hash | +| Signature | 62 bits | Elliptic Curve signature for the RPK hash | +| Auth Key | 10 bits | Backend authentication value | + +However, if we generated a key without the online activation in mind, we still could generate valid keys that would let us through the setup of the operating system. +And that's exactly what the code does - it generates a random 10-bit authentication key. Nowadays it doesn't matter at all, as activation servers are down and +Server 2003 is considered abandonware, the same way this entire project shouldn't be considered piracy. + ### Elliptic Curves Elliptic Curve Cryptography (ECC) is a type of public-key cryptographic system. @@ -111,8 +127,8 @@ OEM keys respectively. The structure of the BINK resource for Windows 98 and Windows XP is as follows: -| Offset | Value | -|-------:|--------------------------------------------------| +| Offset | Value | +|---------:|:-----------------------------------------------| | `0x0000` | BINK ID | | `0x0004` | Size of BINKEY structure in bytes | | `0x0008` | Header length | @@ -131,6 +147,26 @@ The structure of the BINK resource for Windows 98 and Windows XP is as follows: ![BINK](https://github.com/Endermanch/XPKeygen/assets/44542704/497ad018-884f-41af-ba89-633202d30328) +Windows Server 2003 and Windows XP x64 implement it differently: + +| Offset | Value | +|---------:|:-----------------------------------------------| +| `0x0000` | BINK ID | +| `0x0004` | Size of BINKEY structure in bytes | +| `0x0008` | Header length | +| `0x000C` | Checksum | +| `0x0010` | Number-encoded date (BINKEY version) | +| `0x0014` | ECC curve order size (always `12` in practice) | +| `0x0018` | Hash length (always `28` in practice) | +| `0x001C` | Signature length (always `55` in practice) | +| `0x0020` | Finite Field Order `p` | +| `0x005C` | Curve Parameter `a` | +| `0x0098` | Curve Parameter `b` | +| `0x00D4` | Base Point x-coordinate `Gx` | +| `0x0110` | Base Point y-coordinate `Gy` | +| `0x014C` | Public Key x-coordinate `Kx` | +| `0x0188` | Public Key y-coordinate `Ky` | + And here's my implementation for the BINK Reader in C: ```c typedef struct _EC_BYTE_POINT { From a1cd9ec20f8a403c60388e7b9a3517ab275f9b0c Mon Sep 17 00:00:00 2001 From: Andrew <44542704+Endermanch@users.noreply.github.com> Date: Sun, 28 May 2023 15:44:43 +0300 Subject: [PATCH 06/11] Update README.md --- README.md | 70 ++++++++++++++++++++++++++++--------------------------- 1 file changed, 36 insertions(+), 34 deletions(-) diff --git a/README.md b/README.md index 48a7dda..e862aab 100644 --- a/README.md +++ b/README.md @@ -127,45 +127,47 @@ OEM keys respectively. The structure of the BINK resource for Windows 98 and Windows XP is as follows: -| Offset | Value | -|---------:|:-----------------------------------------------| -| `0x0000` | BINK ID | -| `0x0004` | Size of BINKEY structure in bytes | -| `0x0008` | Header length | -| `0x000C` | Checksum | -| `0x0010` | Number-encoded date (BINKEY version) | -| `0x0014` | ECC curve order size (always `12` in practice) | -| `0x0018` | Hash length (always `28` in practice) | -| `0x001C` | Signature length (always `55` in practice) | -| `0x0020` | Finite Field Order `p` | -| `0x005C` | Curve Parameter `a` | -| `0x0098` | Curve Parameter `b` | -| `0x00D4` | Base Point x-coordinate `Gx` | -| `0x0110` | Base Point y-coordinate `Gy` | -| `0x014C` | Public Key x-coordinate `Kx` | -| `0x0188` | Public Key y-coordinate `Ky` | +| Offset | Value | +|---------:|:---------------------------------------------------------------------| +| `0x0000` | BINK ID | +| `0x0004` | Size of BINKEY structure in bytes (always `0x16C` in practice) | +| `0x0008` | Header length (always `7` in practice) | +| `0x000C` | Checksum | +| `0x0010` | Number-encoded date - BINKEY version (always `19980206` in practice) | +| `0x0014` | ECC curve order size (always `12` in practice) | +| `0x0018` | Hash length (always `28` in practice) | +| `0x001C` | Signature length (always `55` in practice) | +| `0x0020` | Finite Field Order `p` | +| `0x005C` | Curve Parameter `a` | +| `0x0098` | Curve Parameter `b` | +| `0x00D4` | Base Point x-coordinate `Gx` | +| `0x0110` | Base Point y-coordinate `Gy` | +| `0x014C` | Public Key x-coordinate `Kx` | +| `0x0188` | Public Key y-coordinate `Ky` | ![BINK](https://github.com/Endermanch/XPKeygen/assets/44542704/497ad018-884f-41af-ba89-633202d30328) Windows Server 2003 and Windows XP x64 implement it differently: -| Offset | Value | -|---------:|:-----------------------------------------------| -| `0x0000` | BINK ID | -| `0x0004` | Size of BINKEY structure in bytes | -| `0x0008` | Header length | -| `0x000C` | Checksum | -| `0x0010` | Number-encoded date (BINKEY version) | -| `0x0014` | ECC curve order size (always `12` in practice) | -| `0x0018` | Hash length (always `28` in practice) | -| `0x001C` | Signature length (always `55` in practice) | -| `0x0020` | Finite Field Order `p` | -| `0x005C` | Curve Parameter `a` | -| `0x0098` | Curve Parameter `b` | -| `0x00D4` | Base Point x-coordinate `Gx` | -| `0x0110` | Base Point y-coordinate `Gy` | -| `0x014C` | Public Key x-coordinate `Kx` | -| `0x0188` | Public Key y-coordinate `Ky` | +| Offset | Value | +|---------:|:---------------------------------------------------------------------| +| `0x0000` | BINK ID | +| `0x0004` | Size of BINKEY structure in bytes | +| `0x0008` | Header length (always `9` in practice) | +| `0x000C` | Checksum | +| `0x0010` | Number-encoded date - BINKEY version (always `20020420` in practice) | +| `0x0014` | ECC curve order size (always `16` in practice) | +| `0x0018` | Hash length (always `31` in practice) | +| `0x001C` | Signature length (always `62` in practice) | +| `0x0020` | Backend authentication value length (always `12` in practice) | +| `0x0024` | Product ID length (always `20` in practice) | +| `0x0028` | Finite Field Order `p` | +| `0x0068` | Curve Parameter `a` | +| `0x00A8` | Curve Parameter `b` | +| `0x00E8` | Base Point x-coordinate `Gx` | +| `0x0128` | Base Point y-coordinate `Gy` | +| `0x0168` | Public Key x-coordinate `Kx` | +| `0x01A8` | Public Key y-coordinate `Ky` | And here's my implementation for the BINK Reader in C: ```c From a8dcf9d702fd2858e5dd78931000f101b8176067 Mon Sep 17 00:00:00 2001 From: Andrew <44542704+Endermanch@users.noreply.github.com> Date: Sun, 28 May 2023 16:06:05 +0300 Subject: [PATCH 07/11] Update README.md --- README.md | 17 ++++++++++++++--- 1 file changed, 14 insertions(+), 3 deletions(-) diff --git a/README.md b/README.md index e862aab..55b8c1d 100644 --- a/README.md +++ b/README.md @@ -12,6 +12,16 @@ Head over to the [**Releases**](https://github.com/Endermanch/XPKeygen/releases) ## *The problem* **In general, the only thing that separates us from generating valid Windows XP keys for EVERY EDITION and EVERY BUILD is the lack of respective private keys generated from their public counterparts inside `pidgen.dll`**. There's no code for the elliptic curve discrete logarithm function widely available online, there's only vague information on how to do it. +The problem has been partially solved. The BINK resource was not encoded in any way and the data was just sequentially written to the resource. **sk00ter** also fully explained the BINK format on the MDL forums. +Utilizing prior community knowledge on the subject, I wrote a BINK Reader in Python 3. The file is public in this repository, [click here](https://github.com/Endermanch/XPKeygen/blob/main/BINKReader.py) to view the source code. + +The discrete logarithm solution is the most unexplored area of research as of **May 28th, 2023**. However, my friend **nephacks** did find that elusive tool to solve that difficult problem in the darkest corners of the internet. +It's called ECDLP (Elliptic Curve Discrete Logarithm Problem) Solver by Mr. HAANDI. Since it was extremely frustrating to find online, I did reupload it on my website. You can download the tool [here](https://dl.malwarewatch.org/software/advanced/ecc-research-tools/). + +The ReadMe file that comes with the version 0.2a of the solver is good enough by itself, so anyone with a brain will be able to set that tool up. + +
+ In the ideal scenario, the keygen would ask you for a BINK-resource extracted from `pidgen.dll`, which it would then unpack into the following segments: * Public key (`pubX`; `pubY`) * Generator (`genX`; `genY`) @@ -22,13 +32,13 @@ Knowing these segments, the keygen would bruteforce the geneator order `genOrder Once the keygen finishes bruteforcing the correct private key, the task boils down to actually generating a key, **which this keygen does**. To give you a better perspective, I can provide you with the flow of the ideal keygen. Crossed out is what my keygen implements: -* BINK resource extraction +* ~~BINK resource extraction~~ * Bruteforce Elliptic Curve discrete logarithm solution (`genOrder`, `privateKey`) * ~~Product Key processing mechanism~~ * ~~Windows XP key generation~~ * ~~Windows XP key validation~~ * ~~Windows Server 2003 key generation~~ -* ~~Windows Server 2003 key validation~~ +
## Principle of operation We need to use a random Raw Product Key as a base to generate a Product ID in a form of `AAAAA-BBB-CCCCCCS-DDEEE`. @@ -145,6 +155,7 @@ The structure of the BINK resource for Windows 98 and Windows XP is as follows: | `0x014C` | Public Key x-coordinate `Kx` | | `0x0188` | Public Key y-coordinate `Ky` | +Each segment is marked with a different color, the BINK header values are the same. ![BINK](https://github.com/Endermanch/XPKeygen/assets/44542704/497ad018-884f-41af-ba89-633202d30328) Windows Server 2003 and Windows XP x64 implement it differently: @@ -169,7 +180,7 @@ Windows Server 2003 and Windows XP x64 implement it differently: | `0x0168` | Public Key x-coordinate `Kx` | | `0x01A8` | Public Key y-coordinate `Ky` | -And here's my implementation for the BINK Reader in C: +And here are my structure prototypes made for the BINK Reader in C: ```c typedef struct _EC_BYTE_POINT { CHAR x[256]; // x-coordinate of the point on the elliptic curve. From 2878ca4aa2a8d8134e2a7ba1059a881e5b341adb Mon Sep 17 00:00:00 2001 From: Andrew <44542704+Endermanch@users.noreply.github.com> Date: Sun, 28 May 2023 16:51:50 +0300 Subject: [PATCH 08/11] Update README.md --- README.md | 54 +++++++++++++++++++++++++++++++++++++++++++++--------- 1 file changed, 45 insertions(+), 9 deletions(-) diff --git a/README.md b/README.md index 55b8c1d..2854e6f 100644 --- a/README.md +++ b/README.md @@ -12,13 +12,15 @@ Head over to the [**Releases**](https://github.com/Endermanch/XPKeygen/releases) ## *The problem* **In general, the only thing that separates us from generating valid Windows XP keys for EVERY EDITION and EVERY BUILD is the lack of respective private keys generated from their public counterparts inside `pidgen.dll`**. There's no code for the elliptic curve discrete logarithm function widely available online, there's only vague information on how to do it. -The problem has been partially solved. The BINK resource was not encoded in any way and the data was just sequentially written to the resource. **sk00ter** also fully explained the BINK format on the MDL forums. +As time went on, the problem has been _partially_ solved. + +The BINK resource was not encoded in any way and the data was just sequentially written to the resource. **sk00ter** also fully explained the BINK format on the MDL forums. Utilizing prior community knowledge on the subject, I wrote a BINK Reader in Python 3. The file is public in this repository, [click here](https://github.com/Endermanch/XPKeygen/blob/main/BINKReader.py) to view the source code. The discrete logarithm solution is the most unexplored area of research as of **May 28th, 2023**. However, my friend **nephacks** did find that elusive tool to solve that difficult problem in the darkest corners of the internet. It's called ECDLP (Elliptic Curve Discrete Logarithm Problem) Solver by Mr. HAANDI. Since it was extremely frustrating to find online, I did reupload it on my website. You can download the tool [here](https://dl.malwarewatch.org/software/advanced/ecc-research-tools/). -The ReadMe file that comes with the version 0.2a of the solver is good enough by itself, so anyone with a brain will be able to set that tool up. +The ReadMe file that comes with the version **0.2a** of the solver is good enough by itself, so anyone with a brain will be able to set that tool up. However, it's not open-source, so integrating it into my keygen is proven impossible.
@@ -223,18 +225,52 @@ typedef struct _BINKEY { In case you want to explore further, the source code of `pidgen.dll` and all its functions is available within this repository, in the "pidgen" folder. -### Generating valid keys +### Reversing the private key -To create the CD-key generation algorithm we must compute the corresponding private key using the public key supplied with `pidgen.dll`, +If we want to generate valid product keys for Windows XP, we must compute the corresponding private key using the public key supplied with `pidgen.dll`, which means we have to reverse-solve the one-way ECC task. -Judging by the key exposed in BINK, p is a prime number with a length of **384 bits**. -The computation difficulty using the most efficient Pollard's Rho algorithm with asymptotic complexity $O(\sqrt{n})$ would be at least $O(2^{168})$, but lucky for us, -Microsoft limited the value of the signature to 55 bits in order to reduce the amount of matching product keys, reducing the difficulty -to a far more manageable $O(2^{28})$. +Judging by the key located in BINK, the curve order is **384 bits** long in Windows XP and **512 bits** long in Server 2003 / XP x64 respectively. +The computation difficulty using the most efficient Pollard's Rho algorithm with asymptotic complexity $O(\sqrt{n})$ would be at least $O(2^{168})$ for Windows XP, and $O(2^{256})$ for Windows Server 2003, but lucky for us, +Microsoft limited the value of the signature to 55 bits in Windows XP and 62 bits in Windows Server 2003 in order to reduce the amount of matching product keys, reducing the difficulty to a far more manageable $O(2^{28})$ / $O(2^{31})$. -The private key was, of course, conveniently computed before us in just 6 hours on a Celeron 800 machine. +As mentioned before, there's only one public tool that satisfies our current needs, which is the ECDLP solver by Mr. HAANDI.
+To compute the private key, we will need to supply the tool with the public ECC values located in the BINK resource, as well as the order `genOrder` of the base point `G(Gx; Gy)`. +The order of the base point can be computed using SageMath. + +**Here's the basic algorithm I used to reverse the Windows 98 private key:** +1. Compute the order of the base point using **SageMath**. In SageMath, execute the following commands: + 1) `E = EllipticCurve(GF(p), [0, 0, 0, a, b])`, where `p`, `a` and `b` are decimally represented elliptic curve parameters from the BINK resource. + 2) `G = E(Gx, Gy)`, where `Gx` and `Gy` are decimally represented base point coordinates from the BINK resource. + 3) `K = E(Kx, Ky)`, where `Kx` and `Ky` are decimally represented public key coordinates from the BINK resource. + 4) `n = G.order()`, `n` will be the computed order of the base point. **It may take some time to compute, even on the newest builds.** + 5) Factor the order using `factor(n)`. Microsoft used prime numbers for the point orders, so if it returns the number itself, it's completely normal. + 6) Save the resulting factors of the order somewhere. + 7) `-K` will give you the inverse of the public key in a projective plane with coordinates `(x : y : z)`. Save the `y` coordinate somewhere, it is required to generate a correct private key. +2. Compute the private key using **ECDLP Solver v0.2a**. + 1) The tool comes with a template job `job_template.txt` and a ReadMe file. It's necessary to understand how the tool works to use it. + 2) Insert all public elliptic curve values from the BINK resource, **except the `Ky` coordinate**. To generate a correct private key, **you must use the inverse coordinate `-Ky` you have calculated in SageMath earlier.** + 3) Insert the factors of the base point order `n` and specify the factor count. It will very likely be `1`, as Microsoft mainly uses primes for their generator orders. + 4) Run the tool ` ECDLP Solver.exe .txt` and wait until it calculates the private key `k = %d` for you. + +Here's an example of the Windows XP job `job_xp.txt` that yields the correct private key for the ECDLP Solver. + +```pascal +GF := GF(22604814143135632990679956684344311209819952803216271952472204855524756275151440456421260165232069708317717961315241); +E := EllipticCurve([GF|1,0]); +G := E![10910744922206512781156913169071750153028386884676208947062808346072531411270489432930252839559606812441712224597826,19170993669917204517491618000619818679152109690172641868349612889930480365274675096509477191800826190959228181870174]; +K := E![14399230353963643339712940015954061581064239835926823517419716769613937039346822269422480779920783799484349086780408,17120082747148185997450361756610881166187863099877353630300913555824935802439591336620545428308962346299700128114607]; +/* +FactorCount:=1; +61760995553426173 +*/ +``` + +And the ECDLP Solver output for it: +![ECDLP Solver Output](https://github.com/Endermanch/XPKeygen/assets/44542704/ca018eae-ae33-41e5-a689-2c17da972184) + +### Validating / generating product keys The rest of the job is done within the code of this keygen. From 45de018a6c95fe468f34cf5416f75381cdc62904 Mon Sep 17 00:00:00 2001 From: Andrew <44542704+Endermanch@users.noreply.github.com> Date: Sun, 28 May 2023 16:58:24 +0300 Subject: [PATCH 09/11] Update README.md --- README.md | 11 +++++++++-- 1 file changed, 9 insertions(+), 2 deletions(-) diff --git a/README.md b/README.md index 2854e6f..28b6f37 100644 --- a/README.md +++ b/README.md @@ -240,6 +240,7 @@ To compute the private key, we will need to supply the tool with the public ECC The order of the base point can be computed using SageMath. **Here's the basic algorithm I used to reverse the Windows 98 private key:** + 1. Compute the order of the base point using **SageMath**. In SageMath, execute the following commands: 1) `E = EllipticCurve(GF(p), [0, 0, 0, a, b])`, where `p`, `a` and `b` are decimally represented elliptic curve parameters from the BINK resource. 2) `G = E(Gx, Gy)`, where `Gx` and `Gy` are decimally represented base point coordinates from the BINK resource. @@ -254,7 +255,7 @@ The order of the base point can be computed using SageMath. 3) Insert the factors of the base point order `n` and specify the factor count. It will very likely be `1`, as Microsoft mainly uses primes for their generator orders. 4) Run the tool ` ECDLP Solver.exe .txt` and wait until it calculates the private key `k = %d` for you. -Here's an example of the Windows XP job `job_xp.txt` that yields the correct private key for the ECDLP Solver. +**Here's an example of the Windows XP job `job_xp.txt` that yields the correct private key for the ECDLP Solver.** ```pascal GF := GF(22604814143135632990679956684344311209819952803216271952472204855524756275151440456421260165232069708317717961315241); @@ -267,9 +268,15 @@ FactorCount:=1; */ ``` -And the ECDLP Solver output for it: +**And the ECDLP Solver output for it:** + ![ECDLP Solver Output](https://github.com/Endermanch/XPKeygen/assets/44542704/ca018eae-ae33-41e5-a689-2c17da972184) +**Important note:** + +Be wary that I could not generate a correct Windows XP x64 key using the private key I've reversed, even using the `Ky` coordinate instead of usual `-Ky`. +For some reason, I also failed to calculate the Windows Server 2003 base point order using SageMath. **I gave it 12 hours to compute on my i7-12700K, but it was still stuck calculating.** + ### Validating / generating product keys The rest of the job is done within the code of this keygen. From 3bed7832ca9ad1c0a6818e6392ec0302a1973f59 Mon Sep 17 00:00:00 2001 From: Andrew <44542704+Endermanch@users.noreply.github.com> Date: Sun, 28 May 2023 17:00:33 +0300 Subject: [PATCH 10/11] Update README.md --- README.md | 10 ++++++---- 1 file changed, 6 insertions(+), 4 deletions(-) diff --git a/README.md b/README.md index 28b6f37..e4a1e83 100644 --- a/README.md +++ b/README.md @@ -126,7 +126,7 @@ An elliptic curve over the finite field Fp consists of: ![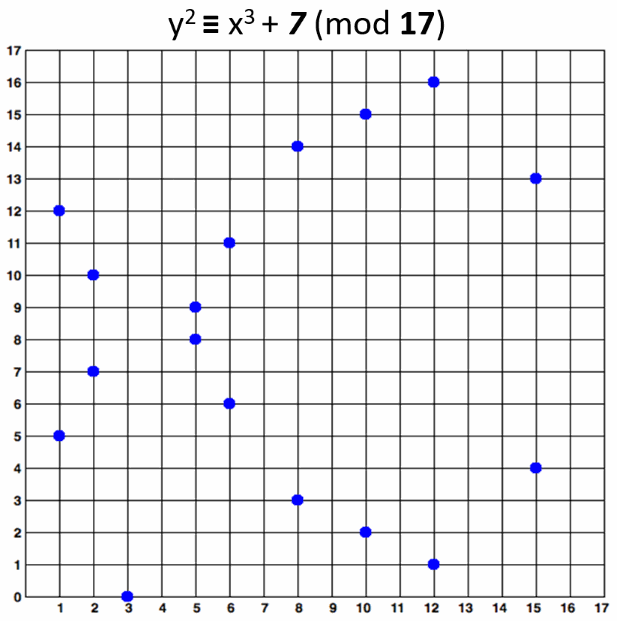F17 Elliptic Curve](https://user-images.githubusercontent.com/44542704/230788993-d340f63c-7201-4307-a52c-9bf159b99d02.png) The curve consists of the blue points in above image. In practice the "elliptic curves" -used in cryptography are "sets of points in square matrix". +used in cryptography are "sets of points in a square matrix". The above curve is "educational". It provides very small key length (4-5 bits). In real world situations developers typically use curves of 256-bits or more. @@ -137,7 +137,7 @@ Since it is a public-key cryptographic system, Microsoft had to share the public It is stored within `pidgen.dll` in a form of a BINK resource. The first set of BINK data is there to validate retail keys, the second is for the OEM keys respectively. -The structure of the BINK resource for Windows 98 and Windows XP is as follows: +**The structure of the BINK resource for Windows 98 and Windows XP is as follows:** | Offset | Value | |---------:|:---------------------------------------------------------------------| @@ -158,9 +158,10 @@ The structure of the BINK resource for Windows 98 and Windows XP is as follows: | `0x0188` | Public Key y-coordinate `Ky` | Each segment is marked with a different color, the BINK header values are the same. + ![BINK](https://github.com/Endermanch/XPKeygen/assets/44542704/497ad018-884f-41af-ba89-633202d30328) -Windows Server 2003 and Windows XP x64 implement it differently: +**Windows Server 2003 and Windows XP x64 implement it differently:** | Offset | Value | |---------:|:---------------------------------------------------------------------| @@ -182,7 +183,8 @@ Windows Server 2003 and Windows XP x64 implement it differently: | `0x0168` | Public Key x-coordinate `Kx` | | `0x01A8` | Public Key y-coordinate `Ky` | -And here are my structure prototypes made for the BINK Reader in C: +**And here are my structure prototypes made for the BINK Reader in C:** + ```c typedef struct _EC_BYTE_POINT { CHAR x[256]; // x-coordinate of the point on the elliptic curve. From 1e106268a932382ad712629797d7a853e1b48164 Mon Sep 17 00:00:00 2001 From: Andrew <44542704+Endermanch@users.noreply.github.com> Date: Sun, 28 May 2023 19:06:23 +0300 Subject: [PATCH 11/11] Update README.md --- README.md | 2 +- 1 file changed, 1 insertion(+), 1 deletion(-) diff --git a/README.md b/README.md index e4a1e83..0dcfe9d 100644 --- a/README.md +++ b/README.md @@ -2,7 +2,7 @@ A Windows XP / Windows Server 2003 VLK key generator. This tool allows you to generate _valid Windows XP keys_ based on the _Raw Product Key_, which can be random. The **Raw Product Key (RPK)** is supplied in form of 9 digits `XXX-YYYYYY` and is only necessary to generate a Windows XP Key. -![image](https://user-images.githubusercontent.com/44542704/231724854-4517f3a1-2330-4e70-83ae-6c52fa1b4745.png) +![Enderman's Keygen](https://github.com/Endermanch/XPKeygen/assets/44542704/bd76ea6a-8bab-4892-8f0a-0cafe529763f) ### Download