# XPKeygen
A command line Windows XP VLK key generator. This tool allows you to generate _valid Windows XP keys_ based on a single
_raw product key_, which can be random. You can also provide the amount of keys to be generated using that raw
product key.
The **Raw Product Key (RPK)** is supplied in a form of 9 digits `XXX-YYYYYY`.
### Download
Check the **Releases** tab and download the latest version from there.
### Principle of operation
We need to use a random Raw Product Key as a base to generate a Product ID in a form of `AAAAA-BBB-CCCCCCS-DDEEE`.
#### Product ID
| Digits | Meaning |
|-------:|:-------------------------------------------------------|
| AAAAA | OS Family constant |
| BBB | Most significant 3 digits of the RPK |
| CCCCCC | Least significant 6 digits of the RPK |
| S | Check digit |
| DD | Index of the public key used to verify the Product Key |
| EEE | Random 3-digit number |
The OS Family constant `AAAAA` is different for each series of Windows XP. For example, it is 76487 for SP3.
The `BBB` and `CCCCCC` sections essentially directly correspond to the Raw Product Key. If the RPK is `XXXYYYYYY`, these two sections
will transform to `XXX` and `YYYYYY` respectively.
The check digit `S` is picked so that the sum of all `C` digits with it added makes a number divisible by 7.
The public key index `DD` lets us know which public key was used to successfully verify the authenticity of our Product Key.
For example, it's 22 for Professional keys and 23 for VLK keys.
A random number `EEE` is used to generate a different Installation ID each time.
#### Product Key
The Product Key itself (not to confuse with the RPK) is of form `FFFFF-GGGGG-HHHHH-JJJJJ-KKKKK`, encoded in Base-24 with
the alphabet `BCDFGHJKMPQRTVWXY2346789` to exclude any characters that can be easily confused, like `I` and `1` or `O` and `0`.
As per the alphabet capacity formula, the key can at most contain 114 bits of information.
$$N = \log_2(24^{25}) \approx 114$$
Based on that calculation, we unpack the 114-bit Product Key into 4 ordered segments:
| Segment | Capacity | Data |
|-----------|----------|-------------------------------------------|
| Flag | 1 bit | Reserved, always set to `0x01`* |
| Serial | 30 bits | Raw Product Key (RPK) |
| Hash | 28 bits | RPK hash |
| Signature | 55 bits | Elliptic Curve signature for the RPK hash |
For simplicity' sake, we'll combine `Flag` and `Serial` segments into a single segment called `Data`. By that logic we'll be able to extract the RPK by
shifting `Data` right and pack it back by shifting bits left.
*It's not fully known what that bit does, but all a priori valid product keys I've checked had it set to 1.
#### Elliptic Curves
Elliptic Curve Cryptography (ECC) is a type of public-key cryptographic system.
This class of systems relies on challenging "one-way" math problems - easy to compute one way and intractable to solve the "other" way.
Sometimes these are called "trapdoor" functions - easy to fall into, complicated to escape.[2]
ECC relies on solving equations of the form
$$y^2 = x^3 + ax + b$$
In general, there are 2 special cases for the Elliptic Curve leveraged in cryptography - **F2m** and **Fp**.
They differ only slightly. Both curves are defined over the finite field, Fp uses a prime parameter that's larger than 3,
F2m assumes $p = 2m$. Microsoft used the latter in their algorithm.
An elliptic curve over the finite field Fp consists of:
* a set of integer coordinates ${x, y}$, such that $0 \le x, y < p$;
* a set of points $y^2 = x^3 + ax + b \mod p$.
**An elliptic curve over F17 would look like this:**
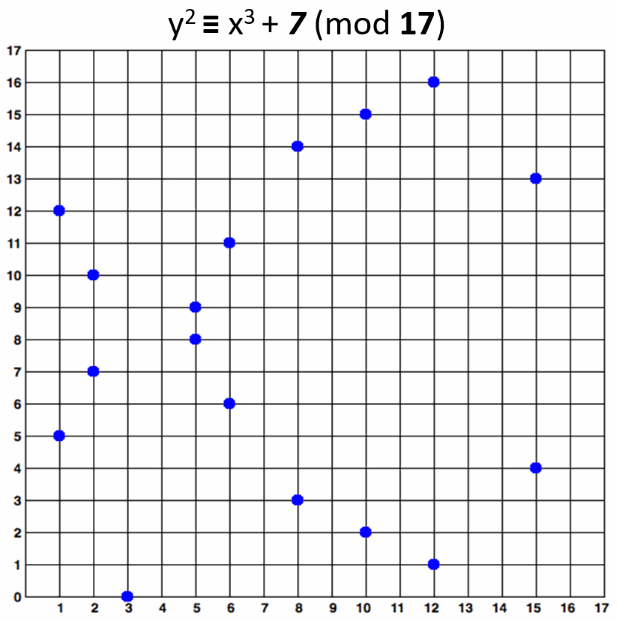
The curve consists of the blue points in above image. In practice the "elliptic curves"
used in cryptography are "sets of points in square matrix".
The above curve is "educational". It provides very small key length (4-5 bits).
In real world situations developers typically use curves of 256-bits or more.
Since it is a public-key cryptographic system, Microsoft had to share the public key with their Windows XP release to check entered product keys against.
It is stored within `pidgen.dll` in a form of a BINK resource. The first set of BINK data is there to validate retail keys, the second is for the
OEM keys respectively.
In case you want to explore further, the source code of `pidgen.dll` and all its functions is available within this repository, in the "pidgen" folder.
#### Generating valid keys
To create the CD-key generation algorithm we must compute the corresponding private key using the public key supplied with `pidgen.dll`,
which means we have to reverse-solve the one-way ECC task.
Judging by the key exposed in BINK, p is a prime number with a length of **384 bits**.
The computation difficulty using the most efficient Pollard's Rho algorithm ($O(\sqrt{n})$) would be at least $O(2^{168})$, but lucky for us,
Microsoft limited the value of the signature to 55 bits in order to reduce the amount of matching product keys, reducing the difficulty
to a far more manageable $O(2^{28})$.
The private key was, of course, conveniently computed before us in just 6 hours on a Celeron 800 machine.
The rest of the job is done within the code of this keygen.
### Known issues
* ~~Some keys aren't valid, but it's generally a less common occurrence. About 2 in 3 of the keys should work.~~
**Fixed in v1.2**. Prior versions generated a valid key with an exact chance of `0x40000/0x62A32`, which resulted in exactly
`0.64884`, or about 65%. My "2 in 3" estimate was inconceivably accurate.
* Tested on multiple Windows XP setups. Works on **Professional x86**, all service packs. Other Windows editions may not work. **x64 DOES NOT WORK**.
* ~~Server 2003 key generation not included yet.~~
**Fixed in v2.2**
* Some Windows XP VLK keys tend to be "worse" than others. Some of them may trigger a broken WPA with an empty Installation ID after install.
You have the best chances generating "better" keys with the `BBB` section set to `640` and the `CCCCCC` section not set to 0.
* Windows Server 2003/SP2 x64 key generation is broken. I'm not sure where to even start there. The keys don't appear to be valid anywhere,
but the algorithm is well-documented. The implementation in my case generates about 1 in 3 "valid" keys. What version they're valid in, we're yet to discover.
### Literature
I will add more decent reads into the bibliography in a later release.
**Understanding basics of Windows XP Activation**:
* [[1] Inside Windows Product Activation - Fully Licensed](https://www.licenturion.com/xp/fully-licensed-wpa.txt)
* [[2] Elliptic Curve Cryptography for Beginners - Matt Rickard](https://matt-rickard.com/elliptic-curve-cryptography)
* [[3] Elliptic Curve Cryptography (ECC) - Practical Cryptography for Developers](https://cryptobook.nakov.com/asymmetric-key-ciphers/elliptic-curve-cryptography-ecc)
**Tested on Windows XP Professional SP3**.
Testing/Issues/Pull Requests welcome.