XPKeygen
A Windows XP / Windows Server 2003 VLK key generator. This tool allows you to generate valid Windows XP keys based on the raw product key, which can be random.
The Raw Product Key (RPK) is supplied in a form of 9 digits XXX-YYYYYY and is only necessary to generate a Windows XP Key.
Download
Head over to the Releases tab and download the latest version from there.
The problem
In general, the only thing that separates us from generating valid Windows XP keys for EVERY EDITION and EVERY BUILD is the lack of respective private keys generated from their public counterparts inside pidgen.dll. There's no code for the elliptic curve discrete logarithm function widely available online, there's only vague information on how to do it.
In the ideal scenario, the keygen would ask you for a BINK-resource extracted from pidgen.dll, which it would then unpack into the following segments:
- Public key (
pubX;pubY) - Generator (
genX;genY) - Base point (
a;b) - Point count
p
Knowing these segments, the keygen would bruteforce the geneator order genOrder using Schoof's algorithm followed by the private key privateKey, leveraging the calculated genOrder to use the most optimal Pollard's Rho algorithm. There's no doubt we can crack any private key in a matter of 20 minutes using modern computational power, provided we have the working algorithm.
Once the keygen finishes bruteforcing the correct private key, the task boils down to actually generating a key, which this keygen does. To give you a better perspective, I can provide you with the flow of the ideal keygen. Crossed out is what my keygen implements:
- BINK resource extraction
- Bruteforce Elliptic Curve discrete logarithm solution (
genOrder,privateKey) Product Key processing mechanismWindows XP key generationWindows XP key validationWindows Server 2003 key generationWindows Server 2003 key validation
Principle of operation
We need to use a random Raw Product Key as a base to generate a Product ID in a form of AAAAA-BBB-CCCCCCS-DDEEE.
Product ID
| Digits | Meaning |
|---|---|
| AAAAA | OS Family constant |
| BBB | Most significant 3 digits of the RPK |
| CCCCCC | Least significant 6 digits of the RPK |
| S | Check digit |
| DD | Index of the public key used to verify the Product Key |
| EEE | Random 3-digit number |
The OS Family constant AAAAA is different for each series of Windows XP. For example, it is 76487 for SP3.
The BBB and CCCCCC sections essentially directly correspond to the Raw Product Key. If the RPK is XXXYYYYYY, these two sections
will transform to XXX and YYYYYY respectively.
The check digit S is picked so that the sum of all C digits with it added makes a number divisible by 7.
The public key index DD lets us know which public key was used to successfully verify the authenticity of our Product Key.
For example, it's 22 for Professional keys and 23 for VLK keys.
A random number EEE is used to generate a different Installation ID each time.
Product Key
The Product Key itself (not to confuse with the RPK) is of form FFFFF-GGGGG-HHHHH-JJJJJ-KKKKK, encoded in Base-24 with
the alphabet BCDFGHJKMPQRTVWXY2346789 to exclude any characters that can be easily confused, like I and 1 or O and 0.
As per the alphabet capacity formula, the key can at most contain 114 bits of information.
N = \log_2(24^{25}) \approx 114
Based on that calculation, we unpack the 114-bit Product Key into 4 ordered segments:
| Segment | Capacity | Data |
|---|---|---|
| Flag | 1 bit | Reserved, always set to 0x01* |
| Serial | 30 bits | Raw Product Key (RPK) |
| Hash | 28 bits | RPK hash |
| Signature | 55 bits | Elliptic Curve signature for the RPK hash |
For simplicity' sake, we'll combine Flag and Serial segments into a single segment called Data. By that logic we'll be able to extract the RPK by
shifting Data right and pack it back by shifting bits left.
*It's not fully known what that bit does, but all a priori valid product keys I've checked had it set to 1.
Elliptic Curves
Elliptic Curve Cryptography (ECC) is a type of public-key cryptographic system. This class of systems relies on challenging "one-way" math problems - easy to compute one way and intractable to solve the "other" way. Sometimes these are called "trapdoor" functions - easy to fall into, complicated to escape.[2]
ECC relies on solving equations of the form
y^2 = x^3 + ax + b
In general, there are 2 special cases for the Elliptic Curve leveraged in cryptography - F2m and Fp.
They differ only slightly. Both curves are defined over the finite field, Fp uses a prime parameter that's larger than 3,
F2m assumes p = 2m. Microsoft used the latter in their algorithm.
An elliptic curve over the finite field Fp consists of:
- a set of integer coordinates
{x, y}, such that0 \le x, y < p; - a set of points
y^2 = x^3 + ax + b \mod p.
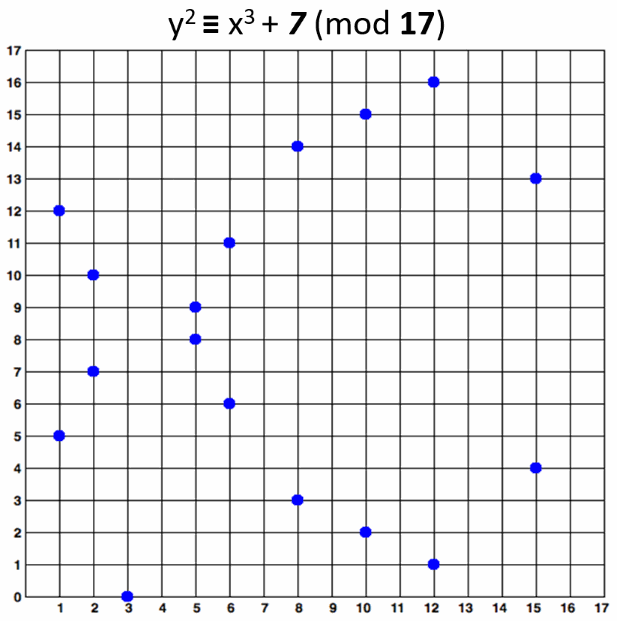
An elliptic curve over F17 would look like this:
The curve consists of the blue points in above image. In practice the "elliptic curves" used in cryptography are "sets of points in square matrix".
The above curve is "educational". It provides very small key length (4-5 bits). In real world situations developers typically use curves of 256-bits or more.
Since it is a public-key cryptographic system, Microsoft had to share the public key with their Windows XP release to check entered product keys against.
It is stored within pidgen.dll in a form of a BINK resource. The first set of BINK data is there to validate retail keys, the second is for the
OEM keys respectively.
In case you want to explore further, the source code of pidgen.dll and all its functions is available within this repository, in the "pidgen" folder.
Generating valid keys
To create the CD-key generation algorithm we must compute the corresponding private key using the public key supplied with pidgen.dll,
which means we have to reverse-solve the one-way ECC task.
Judging by the key exposed in BINK, p is a prime number with a length of 384 bits.
The computation difficulty using the most efficient Pollard's Rho algorithm with asymptotic complexity O(\sqrt{n}) would be at least O(2^{168}), but lucky for us,
Microsoft limited the value of the signature to 55 bits in order to reduce the amount of matching product keys, reducing the difficulty
to a far more manageable O(2^{28}).
The private key was, of course, conveniently computed before us in just 6 hours on a Celeron 800 machine.
The rest of the job is done within the code of this keygen.
Known issues
Some keys aren't valid, but it's generally a less common occurrence. About 2 in 3 of the keys should work.
Fixed in v1.2. Prior versions generated a valid key with an exact chance of0x40000/0x62A32, which resulted in exactly0.64884, or about 65%. My "2 in 3" estimate was inconceivably accurate.- Tested on multiple Windows XP setups. Works on Professional x86, all service packs. Other Windows editions may not work. x64 DOES NOT WORK.
Server 2003 key generation not included yet.
Fixed in v2.2.- Some Windows XP VLK keys tend to be "worse" than others. Some of them may trigger a broken WPA with an empty Installation ID after install.
You have the best chances generating "better" keys with the
BBBsection set to640and theCCCCCCsection not zero. - Windows Server 2003 key generation is broken. I'm not sure where to even start there. The keys don't appear to be valid anywhere, but the algorithm is well-documented. The implementation in my case generates about 1 in 3 "valid" keys.
Literature
I will add more decent reads into the bibliography in later releases.
Understanding basics of Windows XP Activation:
Understanding Elliptic Curve Cryptography:
- [2] Elliptic Curve Cryptography for Beginners - Matt Rickard
- [3] Elliptic Curve Cryptography (ECC) - Practical Cryptography for Developers
- [4] A (Relatively Easy To Understand) Primer on Elliptic Curve Cryptography - Cloudflare
Contributing / Usage
If you're going to showcase or fork this software, please credit Endermanch, z22 and MSKey.
Feel free to modify it to your liking, as long as you keep it open-source. Licensed under GNU General Public License v3.0.
Any contributions or questions welcome.