129 lines
6.7 KiB
Markdown
129 lines
6.7 KiB
Markdown
# XPKeygen
|
|
A command line Windows XP VLK key generator. This tool allows you to generate _valid Windows XP keys_ based on a single
|
|
_raw product key_, which can be random. You can also provide the amount of keys to be generated using that raw
|
|
product key.
|
|
|
|
The **Raw Product Key (RPK)** is supplied in a form of 9 digits `XXX-YYYYYY`.
|
|
|
|
|
|
### Download
|
|
Check the **Releases** tab and download the latest version from there.
|
|
|
|
|
|
### Principle of operation
|
|
We need to use a random Raw Product Key as a base to generate a Product ID in a form of `AAAAA-BBB-CCCCCCS-DDEEE`.
|
|
|
|
#### Product ID
|
|
|
|
| Digits | Meaning |
|
|
|-------:|:-------------------------------------------------------|
|
|
| AAAAA | OS Family constant |
|
|
| BBB | Most significant 3 digits of the RPK |
|
|
| CCCCCC | Least significant 6 digits of the RPK |
|
|
| S | Check digit |
|
|
| DD | Index of the public key used to verify the Product Key |
|
|
| EEE | Random 3-digit number |
|
|
|
|
The OS Family constant `AAAAA` is different for each series of Windows XP. For example, it is 76487 for SP3.
|
|
|
|
The `BBB` and `CCCCCC` sections essentially directly correspond to the Raw Product Key. If the RPK is `XXXYYYYYY`, these two sections
|
|
will transform to `XXX` and `YYYYYY` respectively.
|
|
|
|
The check digit `S` is picked so that the sum of all `C` digits with it added makes a number divisible by 7.
|
|
|
|
The public key index `DD` lets us know which public key was used to successfully verify the authenticity of our Product Key.
|
|
For example, it's 22 for Professional keys and 23 for VLK keys.
|
|
|
|
A random number `EEE` is used to generate a different Installation ID each time.
|
|
|
|
#### Product Key
|
|
|
|
The Product Key itself (not to confuse with the RPK) is of form `FFFFF-GGGGG-HHHHH-JJJJJ-KKKKK`, encoded in Base-24 with
|
|
the alphabet `BCDFGHJKMPQRTVWXY2346789` to exclude any characters that can be easily confused, like `I` and `1` or `O` and `0`.
|
|
|
|
As per the alphabet capacity formula, the key can at most contain 114 bits of information.
|
|
$$N = \log_2(24^{25}) \approx 114$$
|
|
|
|
Based on that calculation, we unpack the 114-bit Product Key into 4 ordered segments:
|
|
|
|
| Segment | Capacity | Data |
|
|
|-----------|----------|-------------------------------------------|
|
|
| Flag | 1 bit | Reserved, always set to `0x01`* |
|
|
| Serial | 30 bits | Raw Product Key (RPK) |
|
|
| Hash | 28 bits | RPK hash |
|
|
| Signature | 55 bits | Elliptic Curve signature for the RPK hash |
|
|
|
|
For simplicity' sake, we'll combine `Flag` and `Serial` segments into a single segment called `Data`. By that logic we'll be able to extract the RPK by
|
|
shifting `Data` right and pack it back by shifting bits left.
|
|
|
|
*It's not fully known what that bit does, but all a priori valid product keys I've checked had it set to 1.
|
|
|
|
#### Elliptic Curves
|
|
Elliptic Curve Cryptography (ECC) is a type of public-key cryptographic system.
|
|
This class of systems relies on challenging "one-way" math problems - easy to compute one way and intractable to solve the "other" way.
|
|
Sometimes these are called "trapdoor" functions - easy to fall into, complicated to escape.<sup>[2]</sup>
|
|
|
|
ECC relies on solving equations of the form
|
|
$$y^2 = x^3 + ax + b$$
|
|
|
|
In general, there are 2 special cases for the Elliptic Curve leveraged in cryptography - **F<sub>2m</sub>** and **F<sub>p</sub>**.
|
|
They differ only slightly. Both curves are defined over the finite field, F<sub>p</sub> uses a prime parameter that's larger than 3,
|
|
F<sub>2m</sub> assumes $p = 2m$. Microsoft used the latter in their algorithm.
|
|
|
|
An elliptic curve over the finite field F<sub>p</sub> consists of:
|
|
* a set of integer coordinates ${x, y}$, such that $0 \le x, y < p$;
|
|
* a set of points $y^2 = x^3 + ax + b \mod p$.
|
|
|
|
**An elliptic curve over F<sub>17</sub> would look like this:**
|
|
|
|
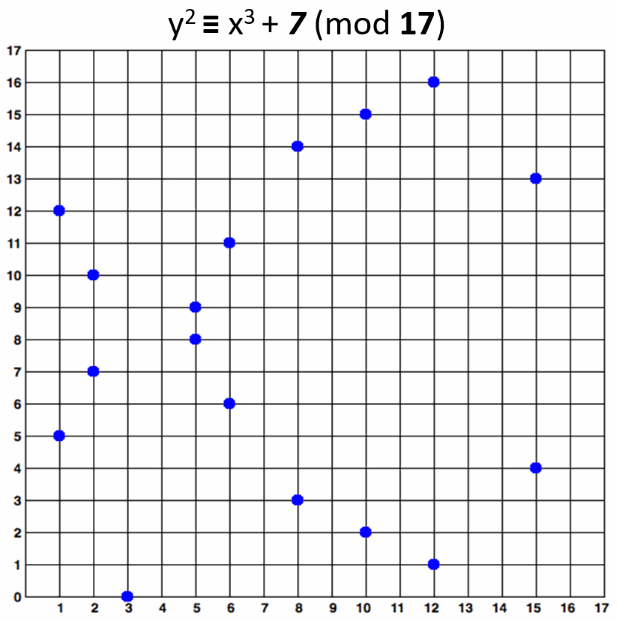
|
|
|
|
The curve consists of the blue points in above image. In practice the "elliptic curves"
|
|
used in cryptography are "sets of points in square matrix".
|
|
|
|
The above curve is "educational". It provides very small key length (4-5 bits).
|
|
In real world situations developers typically use curves of 256-bits or more.
|
|
|
|
|
|
Since it is a public-key cryptographic system, Microsoft had to share the public key with their Windows XP release to check entered product keys against.
|
|
It is stored within `pidgen.dll` in a form of a BINK resource. The first set of BINK data is there to validate retail keys, the second is for the
|
|
OEM keys respectively.
|
|
|
|
In case you want to explore further, the source code of `pidgen.dll` and all its functions is available within this repository, in the "pidgen" folder.
|
|
|
|
#### Generating valid keys
|
|
|
|
To create the CD-key generation algorithm we must compute the corresponding private key using the public key supplied with `pidgen.dll`,
|
|
which means we have to reverse-solve the one-way ECC task.
|
|
|
|
Judging by the key exposed in BINK, p is a prime number with a length of **384 bits**.
|
|
The computation difficulty using the most efficient Pollard's Rho algorithm ($O(\sqrt{n})$) would be at least $O(2^{168})$, but lucky for us,
|
|
Microsoft limited the value of the signature to 55 bits in order to reduce the amount of matching product keys, reducing the difficulty
|
|
to a far more manageable $O(2^{28})$.
|
|
|
|
The private key was, of course, conveniently computed before us in just 6 hours on a Celeron 800 machine.
|
|
|
|
The rest of the job is done within the code of this keygen.
|
|
|
|
|
|
### Known issues
|
|
* ~~Some keys aren't valid, but it's generally a less common occurrence. About 2 in 3 of the keys should work.~~<br>
|
|
**Fixed in v1.2**. Prior versions generated a valid key with an exact chance of `0x40000/0x62A32`, which resulted in exactly
|
|
`0.64884`, or about 65%. My "2 in 3" estimate was inconceivably accurate.
|
|
* Tested **only** on Windows XP Professional SP3, but should work everywhere else as well.
|
|
* Server 2003 key generation not included yet.
|
|
|
|
|
|
### Literature
|
|
I will add more decent reads into the bibliography in a later release.
|
|
|
|
**Understanding basics of Windows XP Activation**:
|
|
* [[1] Inside Windows Product Activation - Fully Licensed](https://www.licenturion.com/xp/fully-licensed-wpa.txt)
|
|
* [[2] Elliptic Curve Cryptography for Beginners - Matt Rickard](https://matt-rickard.com/elliptic-curve-cryptography)
|
|
* [[3] Elliptic Curve Cryptography (ECC) - Practical Cryptography for Developers](https://cryptobook.nakov.com/asymmetric-key-ciphers/elliptic-curve-cryptography-ecc)
|
|
|
|
|
|
**Tested on Windows XP Professional SP3**.
|
|
|
|
Testing/Issues/Pull Requests welcome.
|